Eddiehza's Blog

Appearance

《深度强化学习》读书笔记 ​

INFO

看到卢卢在学于是心血来潮想学 有些内容如果和basic_knowledge重合可能会放到那边去

第一章 机器学习基础 ​

交叉熵 ​

  交叉熵常被用作分类问题的损失函数。它可以用来比较两个模型的差异，因此可以当作损失函数使用。

  使用p=[p1,...,pm]Tp=[p_1, ... ,p_m]^T和q=[q1,...,qm]Tq=[q_1, ... ,q_m]^T表示两个m维的离散概率分布。向量的元素都非负，且∑j=1mpj=1,∑j=1mqj=1\sum_{j=1}^m p_j=1,\sum_{j=1}^m q_j=1。

  交叉熵定义为

H(p,q)=−∑j=1mpj⋅lnqjH(p,q) = -\sum_{j=1}^m p_j\cdot\ln{q_j}

熵&信息量

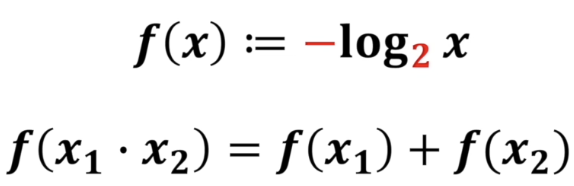alt text   上面是信息量定义。

  熵是交叉熵的一种特例。H(p,p)=−∑j=1mpj⋅lnpjH(p,p) = -\sum_{j=1}^m p_j\cdot\ln{p_j}是概率分布p的熵，可以简写为H(p)H(p)。

  两者都是衡量一个系统从不确定到确定的难度有多大。 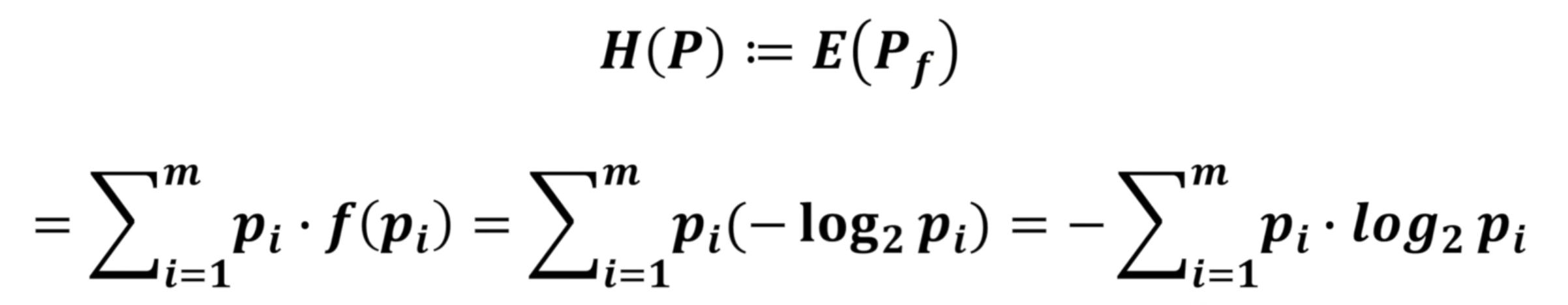alt text   可以看到，熵就是所有事件的信息量分别乘以单独事件在整个系统中发生的概率占比后得到的值，衡量了整个模型的不确定程度，所以可以用于分析训练出来的模型最终是否合理。

KL散度 （相对熵） ​

  用来衡量两个概率分布的区别有多大。KL散度总是非负的，当且仅当p=qp=q，KL(p,q)=0KL(p,q)=0。所以当两个概率分布一致时，他们的KL散度最小。根据上面的补充，可以得知，KL散度实际上是在计算想要两个事件概率达到一样时，还需多少信息量。

  KL散度定义为

KL(p,q)=∑j=1mpj⋅lnpjqjKL(p,q) = \sum_{j=1}^m p_j\cdot\ln\frac{p_j}{q_j}

  可以看出：

KL(p,q)=H(p,q)−H(p)KL(p,q)=H(p,q)-H(p)

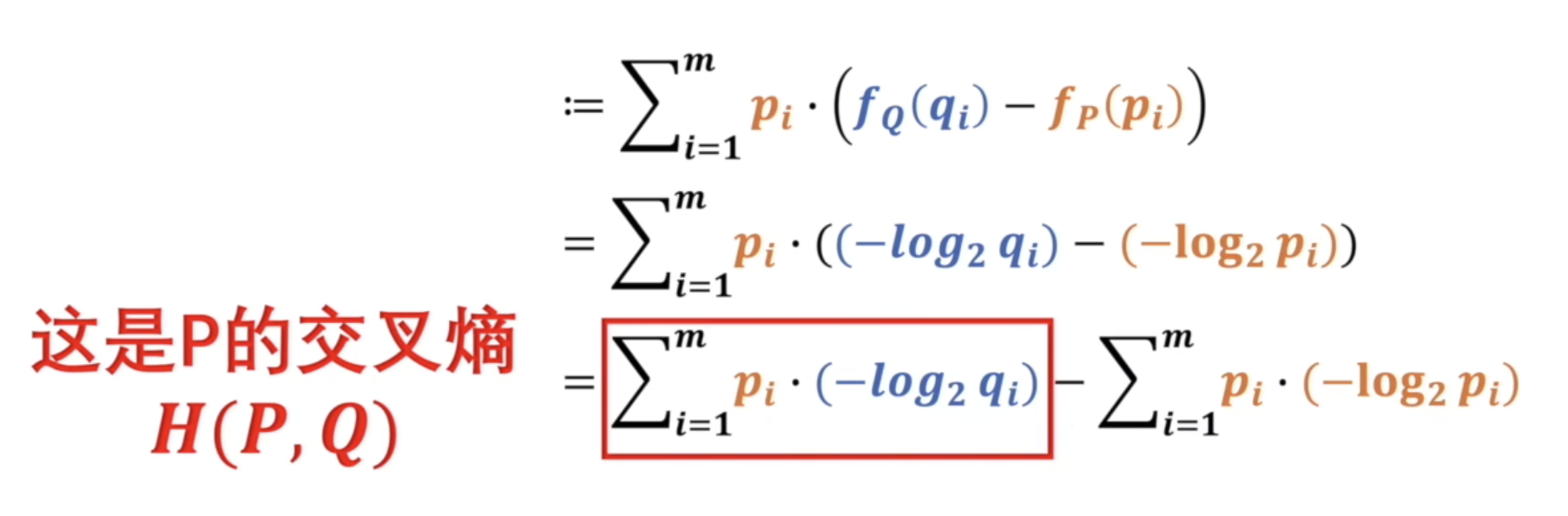alt text   由上其实就可以看出，在熵不变的情况下，交叉熵越小，KL散度越小。

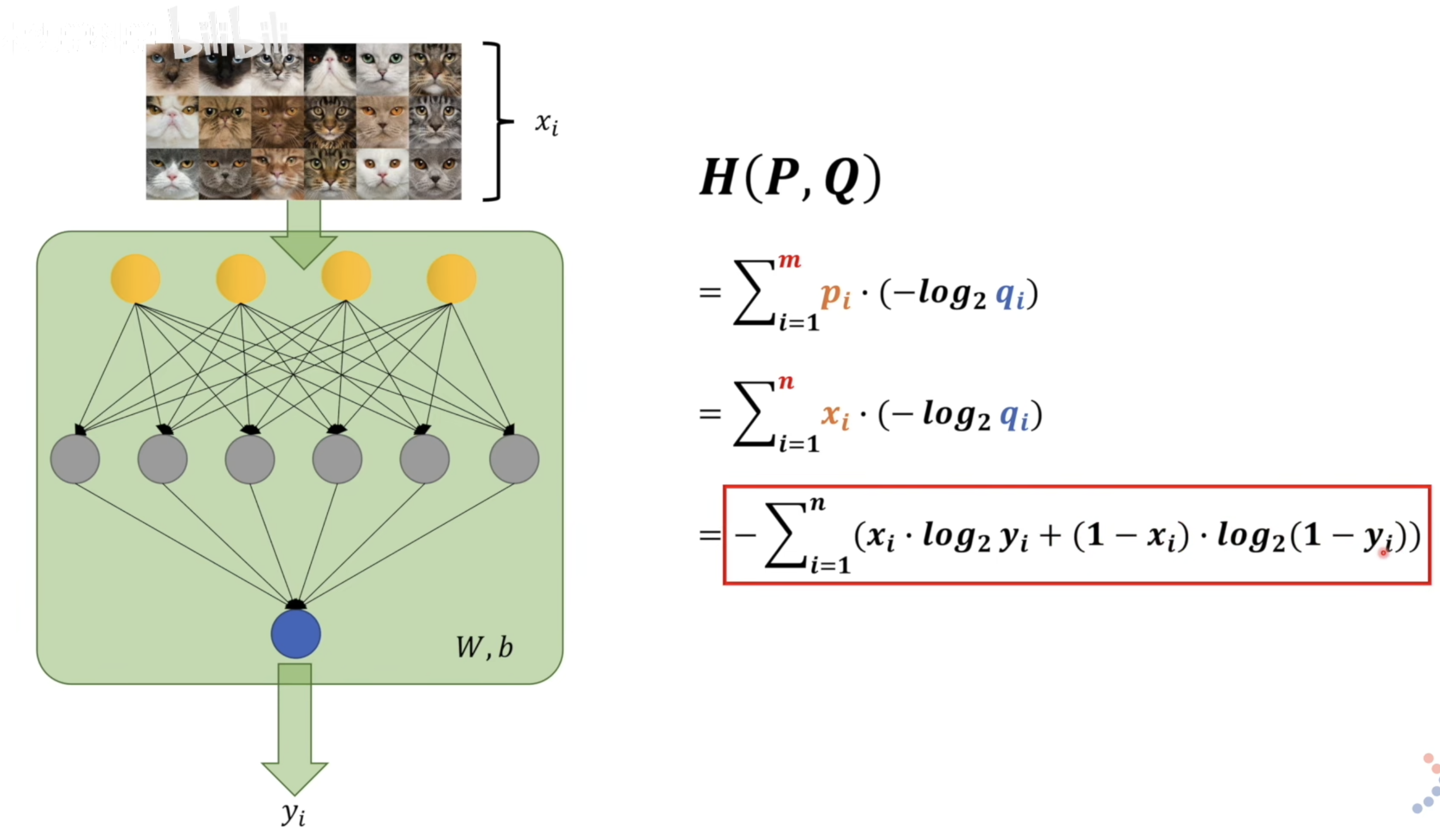alt text   KL用到神经网络里，效果如上。当x为猫（x=1）的时候，取加法前者；当x不为猫（x=0），取后者。所以交叉熵实际上是输入模型和输出模型的差别，两者达到统一还差多少信息量。对我们来说我们希望输出的模型和输入模型是一样的信息量，因此希望KL越小越好。

全连接神经网络 ​

  全连接层就是一个线性函数+激活函数，全连接神经网络由多个全连接层组成，也称为多层感知机。隐层激活函数一般用ReLu函数，输出层（最后一层）的激活函数看情况：二分类用sigmoid，多分类用softmax，回归问题可以不用。

梯度下降 GD ​

  翻基础概念吧

随机梯度下降 SGD ​

  如果目标函数可以写成连加或者期望的形式，就可以用SGD。SGD可以跳出鞍点，趋近局部最优，且计算量明显小于GD。

第二章 蒙特卡罗方法 ​

概率质量函数/概率密度函数 ​

  概率论的东西

期望 ​

  也是概率论。

蒙特卡洛方法 ​

  蒙特卡洛方法是一大类随机算法的总称，通过随机样本来估算真实值。比如求阴影面积，求近似定积分（数值解），说到就是通过落点概率求。

  例如求近似定积分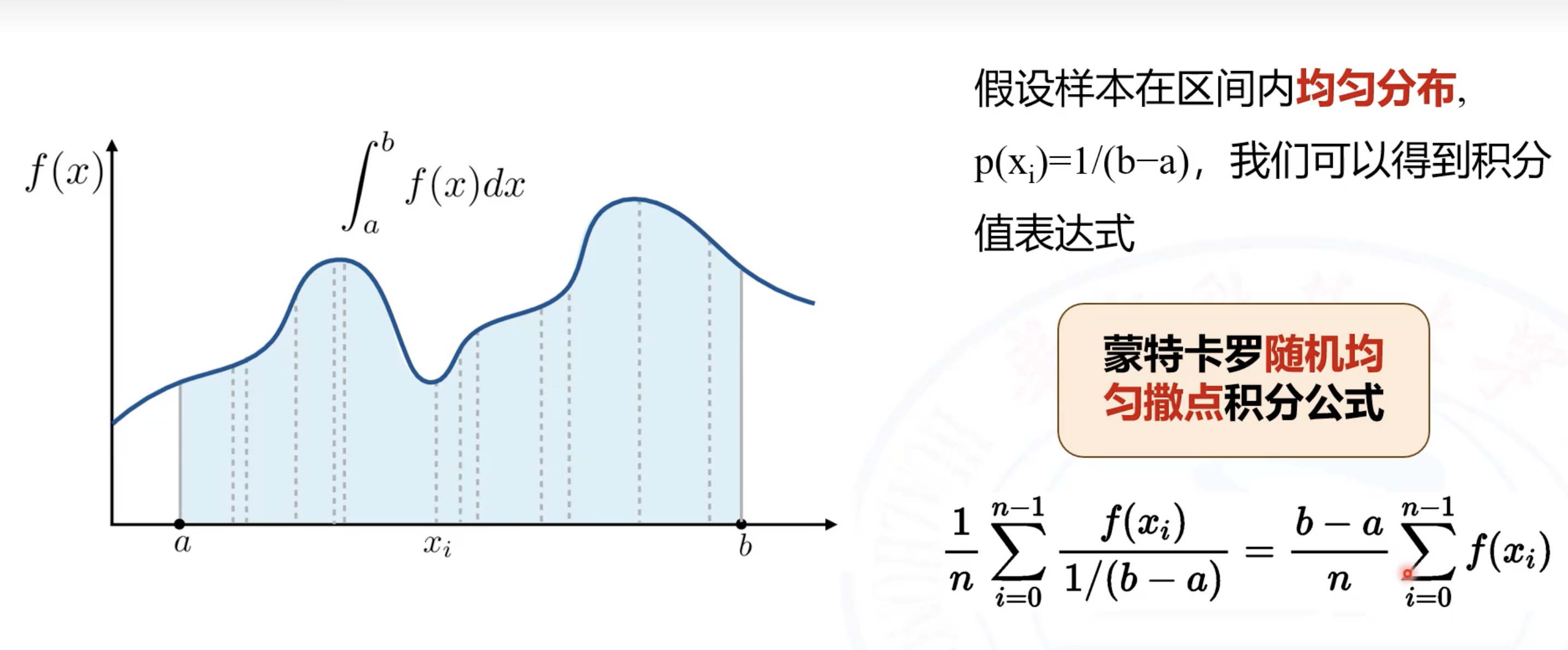： alt text

第三章 强化学习基本概念 ​

相关名词 ​

  • 智能体： 强化学习的主体，即做动作或决策的主体。
  • 环境： 与智能体交互的对象称为。
  • 马尔可夫决策过程 MDP： 强化学习的数学基础和建模工具。一个MDP由状态空间、动作空间、奖励函数、状态转移函数、折扣率等组成。
  • 状态： 每个时刻，环境都有一个状态，可以理解为对当前时刻环境的概括，需要注意是需要囊括所有可能改变未来结局的元素。
  • 状态空间： 所有可能存在的状态的集合，记作花体字母SS。
  • 动作： 智能体基于当前状态所作出的决策。
  • 动作空间： 所有可能动作的集合。
  • 奖励： 智能体执行一个动作之后，环境返回给智能体的一个数值。是状态和动作的函数。rt=r(st,at)r_t=r(s_t,a_t)
  • 状态转移： 智能体从当前t时刻的状态s转移到下一个时刻的状态s'的过程。这个过程可能是随机的，随机性来自环境。例如，我躲避敌人的子弹，我躲避的动作和时间是确定的，但是敌人开枪并不是确定的，因此我的下一个状态也是不确定的。
  • 策略： 如何根据观测到的状态做出决策，即如何从动作空间中选取一个动作。
  • 最优策略： 寻找一个策略，使得回报的期望最大化。
  • 回合： 强化学习的概念，与监督学习的epoch不同。回合指游戏中的一个过程，epoch指使用训练数据进行前行计算和反向计算。
  • 轨迹： 一个回合中，智能体观测到的所有状态、动作、奖励

策略 ​

  这是强化学习的目标。分为随机性策略和确定性策略。随机性指算出每个动作的概率值，然后随机抽样；确定性策略则直接选择特定的那一个动作。

随机性 ​

  动作的随机性来自于策略。智能体执行的动作是随机抽样的结果，所以带有随机性。

  状态的随机性来源于状态转移。指下一个状态不会因为当前状态和动作的确定而确定。

马尔可夫性质 ​

P(St+1∣St,At)=P(St+1∣S1,A1,S2,A2,...,St,At)P(S_{t+1}|S_t,A_t)=P(S_{t+1}|S_1,A_1,S_2,A_2,...,S_t,A_t)

  即下一时刻的状态仅依赖于当前状态和动作，与过去状态和动作无关。

回报与折扣汇报 ​

  回报是指从当前时刻开始到本回合结束的所有奖励的总和，也称作累计奖励。强化学习目标是为了最大化回报，而不是最大化当前奖励。

  折扣回报是指给未来的奖励打折扣。定义一个折扣率γ\gamma，对未来的奖励进行打折。折扣回报的定义如下：

Ut=Rt+γ⋅Rt+1+γ2⋅Rt+2+...,γ∈[0,1]U_t = R_t + \gamma \cdot R_{t+1}+ \gamma^2 \cdot R_{t+2}+..., \gamma \in [0,1]

  由于回报依赖于未来的状态和动作，而动作和状态具有随机性，因此依赖于不确定的动作和状态的回报也具有随机性。

有限期MDP和无限期MDP ​

  MDP的时间步可以是有限期或者无限期的。有限期的存在一个终止状态，该状态被智能体触发以后，一个回合结束。无限期不存在终止状态，这会导致奖励的和趋于无穷大（γ\gamma=1）。因此，我们需要定义一个奖励函数的上界b，使得∣r(s,a)∣<b|r(s,a)|<b，即:

∣limn→∞∑i=tnγi−tri∣≤b1−γ|\lim_{n \to \infty}\sum_{i=t}^n \gamma^{i-t}r_i|\leq\frac{b}{1-\gamma}

价值函数 ​

  价值函数是回报的期望，即未来期望获得的奖励之和。价值函数反映现状的好坏。

  • 动作价值函数： 在假设t时刻执行某一动作后，得到的回报期望。
  • 最优动作价值函数： 排除策略影响，评价当前状态下各动作带来的最大回报期望，选择最大的那个。
  • 状态价值函数： 在当前状态下，来量化最终的胜算。

第四章 DQN与Q学习 ​

DQN 深度Q网络 ​

  用神经网络近似最优动作价值函数 Q⋆(s,a)Q_\star(s,a)。动作价值函数的定义是：

Qπ(st,at)=E[Ut∣St=st,At=at]Q_\pi(s_t,a_t) = E[ U_t|S_t=s_t,A_t=a_t ]

  上式中的期望消除了t时刻后的所有状态S_{t+1},...,S_n与所有动作A_{t+1},...A_n。最优动作价值函数使用最大化消除策略π\pi：

Q⋆(st,at)=maxπQπ(st,at),∀st∈S,at∈AQ_{\star}(s_t,a_t) = \max_\pi Q_\pi(s_t,a_t), \forall s_t \in S, a_t \in A

  虽然预知未来很难，但是如果类似于一个游戏，我们其实可以玩上亿次，把每一步每种情况都尝试一遍，理论上就能训练出我们想要的效果。

DQN表达式 ​

  使用DQN去近似学习先知Q⋆Q_\star，记作Q(s,a;ω)Q(s,a;\omega)，其中ω\omega代表了神经网络中的参数，先随机初始化，后根据经验进行学习。DQN的输出是离散动作空间A中的每个动作的Q值，即给每个动作的评分。

  DQN由卷积神经网络和全连接神经网络组成。卷积神经网络我的理解是在提取特征点。

TD 时间差分算法 ​

  先不聊TD，先举个例子：地图模型一开始不准确，但是随着越来越多的人用这个模型，上传的数据越多这个地图模型越准。例如预测我从上海到北京的时间，在我的实际数据上传后，用梯度下降对模型进行更新。用实际耗时和模型最开始预测耗时的方差作为损失函数，然后用链式法则计算损失函数的梯度，然后梯度下降。（其实就是最普通的模型训练）

  但是如果我没有完成旅途，就可以用到TD帮助模型的训练。例如预测上海到北京要14个小时，我到济南实际用时4个小时，预测济南到北京还要11个小时，那么可以看出，最新估计为4+11=15个小时，虽然这个数据不准，但是也比原先14个小时准了，就可以用这个数据进行训练。15被称为TD目标。15-14=1被称为TD误差。

知识补充

  TD算法是一大类算法，常见的有Q学习和SARSA。DQN是神经网络形式的Q学习。

  Q学习的目的是学到最优动作价值Q⋆Q_\star，而SARSA的目的是为了学习动作价值函数QπQ_\pi。

最优贝尔曼方程 ​

Q⋆(st,at)=ESt+1∼p(⋅∣st,at)[Rt+γ⋅maxA∈AQ⋆(St+1,A)∣St=st,At=at]Q_\star(s_t,a_t)=E_{S_{t+1} \sim p(\cdot|s_t,a_t)} [ R_t + \gamma \cdot \max_{A\in A} Q_\star(S_{t+1},A)|S_t=s_t,A_t=a_t ]

  最优贝尔曼方程右边是一个期望，可以用蒙特卡洛方法近似。

同策略/异策略/行为策略/目标策略 ​

  • 行为策略： 智能体与环境交互，记录观测到的状态、动作和奖励，并学习一个策略函数，以此控制智能体与环境交互的策略。
  • 目标策略： 通过强化学习得到一个策略函数，来控制智能体。
  • 同策略： 行为策略和目标策略相同。
  • 异策略： 行为策略和目标策略不同。

  由于Q学习算法用任意的行为策略收集信息，然后训练目标策略，即DQN，因此Q学习和DQN都属于异策略。异策略的好处是可以用行为策略收集经验，存到一个缓存里，事后反复使用这些经验去更新目标策略。这个缓存称为经验回放缓存。这种将智能体与环境交互的记录暂时保存，然后从中采样和学习的训练方式称为经验回放。经验回放只适用于异策略，因为收集经验时用的行为策略不同于想要训练出的目标策略。